Геометрическое место середин хорд на окружности — олимпиадная задача по планиметрии
Задача
ТочкиAиB, лежащие на окружности разбивают её на две дуги. Найдите геометрическое место середин всевозможных хорд, концы которых лежат на разных дугахAB.
Решение
Пусть K – произвольная точка внутри данной окружности. Хорда, серединой которой является K, перпендикулярна OK. Поэтому она пересекает отрезок AB тогда и только тогда, когда один из углов OKA, OKB не острый, а другой – не тупой (см. рис. слева). Следовательно, искомое множество состоит из точек, лежащих внутри или на границе одного из кругов с диаметрами OA, OB и вне или на границе другого (рис. справа).
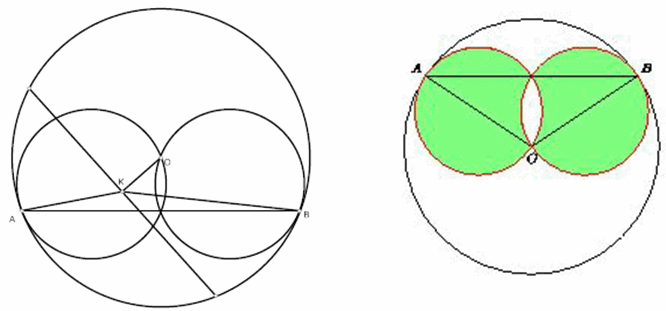
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет