Задача
Дано уравнение xn – a1xn–1 – a2xn–2 – ... – an–1x – an = 0, где a1 ≥ 0, a2 ≥ 0, an ≥ 0.
Доказать, что это уравнение не может иметь двух положительных корней.
Решение
Перепишем данное уравнение в виде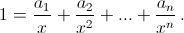 
При x > 0 функция в правой части монотонно убывает, поэтому она не может принимать значение 1 при двух различных положительных значениях x.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет