Задача
Какому условию должны удовлетворять коэффициенты a, b, c уравнения x³ + ax² + bx + c, чтобы три его корня составляли арифметическую прогрессию?
Решение
Пусть x1 ≤ x2 ≤ x3 – корни нашего уравнения. Тогда x1 + x2 + x3 = – a. Для того чтобы x1, x2, x3 составляли арифметическую прогрессию, необходимо и достаточно, чтобы x1 + x3 = 2x2. Поэтому x2 = – a/3, x1 + x3 = – 2a/3.
Далее,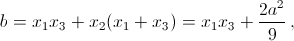 
то есть 
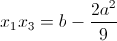. Значит,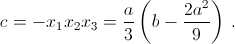 
Чтобы корни были действительными, система x1 + x3 = – 2a/3, 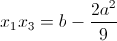должна иметь действительные решения, то есть трёхчлен 
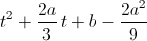должен иметь неотрицательный дискриминант. Отсюда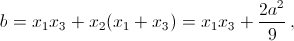 
Ответ
27c = 3ab – 2a³, 3b ≤ a².
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет