Назад

Олимпиадная задача по планиметрии: выпуклость пятиугольника из биссектрис

Задача 209947 • Сложность: 3 • 8-10 класс
Задача

В пятиугольнике A1A2A3A4A5 проведены биссектрисы l1, l2, ..., l5 углов A1, A2, ..., A5 соответственно. Биссектрисы l1 и l2 пересекаются в точке B1, l2 и l3 – в точке B2 и т.д., ..., l5 и l1 пересекаются в точке B5. Может ли пятиугольник B1B2B3B4B5 оказаться выпуклым?

Авторы:
Смирнова Л. Тарасенко Д.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 1997-1998 Региональный этап
Количество версий:
5
Решение

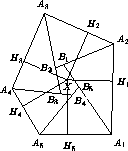
Предположим, что пятиугольник B1B2B3B4B5 – выпуклый. Возьмём внутри него точку X и опустим из неё на прямые A1A2, A2A3, ..., A5A1 перпендикуляры XH1, XH2, ..., XH5 соответственно (см. рис.).

Из расположенияXотносительно биссектрис угловAiследует, что  XH1<XH2<XH3<XH4<XH5<XH1.  Противоречие.
Ответ

Не может.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет