Олимпиадная задача по стереометрии: угол между прямой BD₁ и плоскостью BDC₁ (10–11 класс)
Задача
Основанием прямоугольного параллелепипеда АВСDA1B1C1D1 является квадрат АВСD.
Найдите наибольшую возможную величину угла между прямой BD1 и плоскостью ВDС1.
Решение
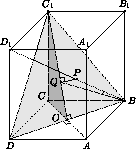
Рассмотрим сечение ВDС1 данного параллелепипеда (см. рис. слева). Пусть О – точка пересечения диагоналей квадрата АВСD. Так как треугольник DC1B – равнобедренный, то C1О – его высота. Пусть Р – точка пересечения диагоналей параллелепипеда, РQ – перпендикуляр к плоскости ВDС1. Ясно, что точка Р равноудалена от вершин треугольника DC1B, поэтому Q – центр описанной около него окружности. Так как этот треугольник – остроугольный и равнобедренный, точка Q лежит на отрезке C1О. Углом между прямой BD1 и плоскостью ВDС1 является острый угол α между (BD1) и её ортогональной проекцией на (ВDС1), то есть угол РВQ.
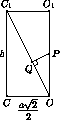
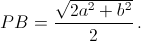 ДлинуРQможно найти, рассмотрев, например, прямоугольникСС1О1О, гдеО1– точка пересечения диагоналей квадратаА1В1С1D1(см. рис. справа). Из подобия прямоугольных треугольниковРОQиС1ОО1получим, что
ДлинуРQможно найти, рассмотрев, например, прямоугольникСС1О1О, гдеО1– точка пересечения диагоналей квадратаА1В1С1D1(см. рис. справа). Из подобия прямоугольных треугольниковРОQиС1ОО1получим, что 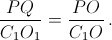 Так как
Так как 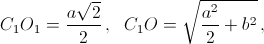 то
то 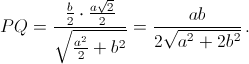 Следовательно,
Следовательно,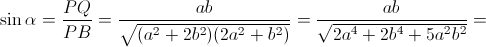
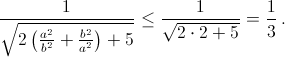
Ответ
arcsin ⅓.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь