Олимпиадная задача про "сокращение" дробей Ваней: двухцифровые числа для 7–9 классов

  Рассмотрим все возможные случаи сокращений.   1) 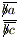 .  Получаем  (10b + a)c = (10b + c)a,  bc = ba.  b ≠ 0,  следовательно,  c = a,  а по условию дробь правильная. Поэтому решений нет.   2)  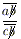.   Аналогично первому случаю получаем, что решений тоже нет.   3)  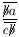.   Получаем  (10b + a)c = (10c + b)a,  откуда  9c(a – b) = b(c – a).  Так как дробь правильная, то  a < c.  Следовательно,  a > b,  откуда  a – b ≥ 1.

9c(a – b) ≥ 9c > 9(c – a) ≥ b(c – a), то есть  9c(a – b) > b(c – a),  что невозможно.   4) 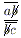 .   Тогда  (10a + b)c = (10b + c)a,  откуда  9a(b – c) = b(c – a).  Как в предыдущем случае замечаем, что  b > c > a.  Значит,  c – a  не может равняться 9, поэтому b кратно 3.

  Если  b = 3,  то  c = 2,  a = 1.  Но эти значения не удовлетворяют уравнению.

  Если  b = 6,  то  c – a = 3,  откуда  c = 5,  a = 2  или  c = 4,  a = 3.  Оба варианта годятся.

  Если  b = 9,  то  a(9 – c) = c – a,  то есть  10a = c(a + 1).  Так как a и  a + 1  взаимно просты, то 10 делится на  a + 1.  Значит,  a = 1  или  a = 4,  откуда, соответственно,  c = 5  или  с = 8.

²⁶/₆₅, ¹⁶/₆₄, ¹⁹/₉₅, ⁴⁹/₉₈.