Олимпиадная задача по математике: разбиение треугольников и равенство площадей
Задача
Даны три треугольника: A1A2A3, B1B2B3, C1C2C3. Известно, что их центры тяжести (точки пересечения медиан) лежат на одной прямой, а никакие три из девяти вершин этих треугольников не лежат на одной прямой. Рассматриваются 27 треугольников вида AiBjCk, где i, j, k независимо пробегают значения 1, 2, 3. Докажите, что эти 27 треугольников можно разбить на две группы так, что сумма площадей треугольников первой группы будет равна сумме площадей треугольников второй группы.
Решение
Будем рассматривать ориентированную площадь треугольников, считая SMNK положительной, если обход M → N → K совершается против часовой стрелки. Заметим что для таких площадей выполнено равенство SMNA + SMNB + SMNC = 3SMNT, где T – центр тяжести треугольника ABC. Для доказательства достаточно ввести систему координат, где ось абсцисс совпадает с прямой MN. Тогда (при фиксированных M и N) площадь SMNK пропорциональна ординате точки K, а ордината центра тяжести – среднее арифметическое ординат вершин треугольника.
Обозначим P, Q, R центры масс треугольников A1A2A3, B1B2B3, C1C2C3.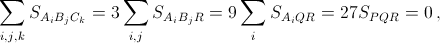 
то есть сумма всех "положительных" площадей равна сумме всех "отрицательных".
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь