Задача
Каждая грань выпуклого многогранника – многоугольник с чётным числом сторон.
Обязательно ли его рёбра можно раскрасить в два цвета так, чтобы у каждой грани было поровну рёбер разных цветов?
Решение
Пусть M – многогранник, рёбра которого покрашены требуемым образом. Если i-м (i = 1, 2) цветом покрашено ni рёбер, то суммарное (по всем граням) число сторон этого цвета равно 2ni (каждое ребро служит стороной ровно двум граням). А так как у каждой грани сторон разных цветов поровну, то 2n1 = 2n2, то есть n1 = n2, и общее число рёбер n1 + n2 чётно.
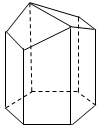
На рисунке показан девятигранник, имеющий 19 рёбер и ограниченный одной шестиугольной и восемью четырёхугольными гранями. Согласно вышедоказанному раскрасить его рёбра нужным образом нельзя.
Ответ
Не обязательно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь