Задача
Считая известной формулу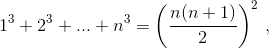 
доказать, что для различных натуральных чисел a1, a2, ..., an справедливо неравенство 
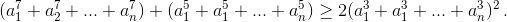Возможно ли равенство для каких-нибудь различных натуральных чисел a1, a2, ..., an?
Решение
Доказательство проведём по индукции. База: a7 + a5 ≥ 2a6 ⇔ a5(a − 1)² ≥ 0.
Шаг индукции. Пусть a1 < ... < an+1 – произвольные натуральные числа. По предположению индукции 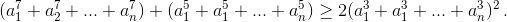Но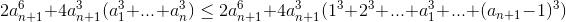 
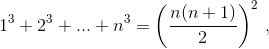(здесь мы существенно использовали, что все аi различны). Сложив эти неравенства, получим: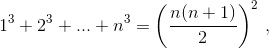 
Равенство справедливо при a1 = 1, а2 = 2, ..., аn = n. Это доказывается по индукции тем же способом, только все неравенства превращаются в равенства.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет