Задача
При каких натуральных n ≥ 2 неравенство 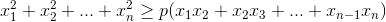 выполняется для любых действительных чисел x1, x2, ..., xn, если
выполняется для любых действительных чисел x1, x2, ..., xn, если
а) p = 1;
б) p = 4/3;
в) p = 6/5?
Решение
Заметим, что если положить в неравенстве 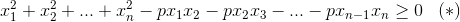 несколько последних переменных xk, xk+1, ..., xn равными нулю, то получится аналогичное неравенство, соответствующее меньшему n . Отсюда следует, что если () выполняется (для всех x1, x2, ..., xn) при некотором n , то оно выполняется и при меньших n. Таким образом, для каждого фиксированного p существует таксе целое N(p) ≥ 2, что () выполнено при n < N(p) и не выполнено (для некоторых x1, x2 , ..., xn) при n ≥ N(p); возможно также, что () выполнено при всех n (в этом случае можно считать, что N(p) = ∞). а) При p = 1 неравенство () эквивалентно очевидному неравенству
несколько последних переменных xk, xk+1, ..., xn равными нулю, то получится аналогичное неравенство, соответствующее меньшему n . Отсюда следует, что если () выполняется (для всех x1, x2, ..., xn) при некотором n , то оно выполняется и при меньших n. Таким образом, для каждого фиксированного p существует таксе целое N(p) ≥ 2, что () выполнено при n < N(p) и не выполнено (для некоторых x1, x2 , ..., xn) при n ≥ N(p); возможно также, что () выполнено при всех n (в этом случае можно считать, что N(p) = ∞). а) При p = 1 неравенство () эквивалентно очевидному неравенству 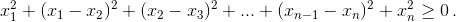 . Значит, N(1) = ∞. б) При p = 4/3 и n = 3 неравенство () эквивалентно неравенству
. Значит, N(1) = ∞. б) При p = 4/3 и n = 3 неравенство () эквивалентно неравенству 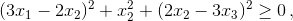 а при n = 4 неравенство () нарушается, например, когда x1 = x4 = 2, x2 = x3 = 3. в) При p = 6/5 и n = 4 (*) эквивалентно неравенству
а при n = 4 неравенство () нарушается, например, когда x1 = x4 = 2, x2 = x3 = 3. в) При p = 6/5 и n = 4 (*) эквивалентно неравенству 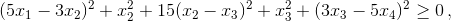 а при n = 5 оно нарушается, например, когда x1 = x5 = 9, x2 = x4 = 15, x3 = 16.
а при n = 5 оно нарушается, например, когда x1 = x5 = 9, x2 = x4 = 15, x3 = 16.
Ответ
а) При всех n; б) при n ≤ 3; в) при n ≤ 4.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь