Задача
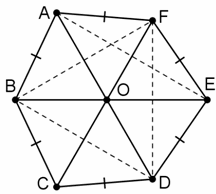
В выпуклом шестиугольнике ABCDEF все стороны равны, а также AD = BE = CF. Докажите, что в этот шестиугольник можно вписать окружность.
Решение
Поскольку треугольники ABD и EDB равны по трём сторонам, то четырёхугольник ABDE – равнобокая трапеция или прямоугольник. Её ось симметрии – серединный перпендикуляр к основаниям BD и AE. На этом же перпендикуляре лежат и вершины C и F равнобедренных треугольников BCD и AFE. Аналогично прямые AD и BE являются осями симметрии шестиугольника. Все три оси пересекаются в центре O описанной окружности треугольника BDF. Так как биссектрисы всех углов многоугольника пересекаются в одной точке, то его стороны равноудалены от неё.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет