Задача
Планета "Тетраинкогнито", покрытая "океаном", имеет форму правильного тетраэдра с ребром 900 км.
Какую площадь океана накроет "цунами" через 2 часа после тетратрясения с эпицентром в
а) центре грани,
б) середине ребра,
если скорость распространения цунами 300 км/час?
Решение
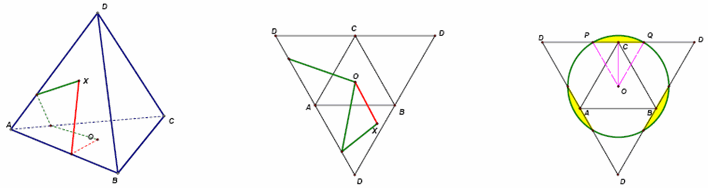
а) Рассмотрим развёртку в виде правильного треугольника и докажем, что кратчайший путь из его центра в любую точку будет на этой развертке отрезком. Пусть O – центр грани ABC, X – точка на грани ABD и некоторый путь из O в X пересекает сначала ребро AC (рис. слева). Если продолжить этот путь на развёртке, мы попадём в некоторую точку на ребре AD. Но в эту точку ведёт и путь через ребро AB, через которое в X можно попасть напрямую (рис. в центре).
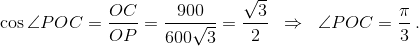 Площадь сегмента есть разность площадей сектора и треугольника:
Площадь сегмента есть разность площадей сектора и треугольника: 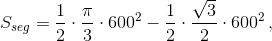 откуда искомая площадь равна
откуда искомая площадь равна  б) Рассматривая "двойную" развертку тетраэдра и рассуждая, как в предыдущем случае, убеждаемся в том, что кратчайшие пути лежат внутри заштрихованного прямоугольника.
б) Рассматривая "двойную" развертку тетраэдра и рассуждая, как в предыдущем случае, убеждаемся в том, что кратчайшие пути лежат внутри заштрихованного прямоугольника.
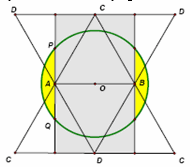
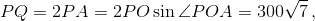
 а искомая площадь равна
а искомая площадь равна 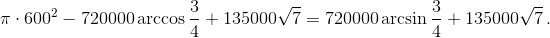
Ответ
а) 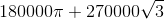 км²; б)
км²; б) 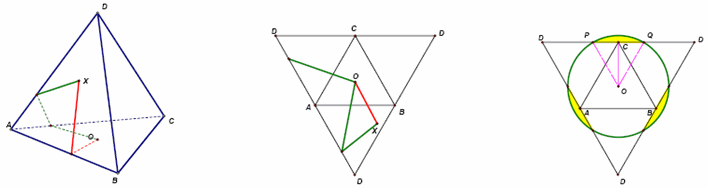 км².
км².
Чтобы оставлять комментарии, войдите или зарегистрируйтесь