Для удобства сделаем замену  x = 2a  и  y = 2b.  Тогда  a¹⁰⁰ – b¹⁰⁰ = a²⁰⁰ – b²⁰⁰ = a – b ≠0.  Поделив второе выражение на первое, получаем

a¹⁰⁰ + b¹⁰⁰ = 1;  значит, каждое из чисел a и b по модулю не превосходит 1.

  Если  b = 0,  то  a¹⁰⁰ = a,  откуда  a = 1.  Аналогично если  a = 0,  то  b = 1.

  Пусть теперь  ab ≠ 0;  тогда  0 < |a|, |b| < 1.  Заметим, что значения функции  f(x) = x¹⁰⁰ – x = x(x⁹⁹ – 1)  положительны при  x ∈ (–1, 0)  и отрицательны при  x ∈ (0, 1).  Поскольку  a¹⁰⁰ – b¹⁰⁰ = a – b,  имеем  f(a) = f(b),  поэтому числа a и b имеют одинаковый знак.

  С другой стороны,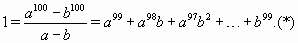  

  Если a и b отрицательны, то правая часть в () также отрицательна, что невозможно. Если же a и b положительны, то все слагаемые в правой части () положительны, поэтому она больше чем  a⁹⁹ + b⁹⁹;  итак,  a⁹⁹ + b⁹⁹ < 1.  С другой стороны, поскольку  0 < |a|, |b| < 1,  то  a⁹⁹ + b⁹⁹ > a¹⁰⁰ + b¹⁰⁰ = 1.  Противоречие.

(2, 0)  и  (0, 2).