Задача
Уравнение с целыми коэффициентами x4 + ax³ + bx² + cx + d = 0 имеет четыре положительных корня с учетом кратности.
Найдите наименьшее возможное значение коэффициента b при этих условиях.
Решение
Пусть x1, x2, x3, x4 – корни уравнения (возможно, некоторые из них совпадают). По теореме Виета b = x1x2 + x1x3 + x1x4 + x2x3 + x2x4 + x3x4,
d = x1x2x3x4, а значит, b и d положительны. Заметим, что
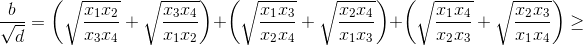 2 + 2 + 2 (неравенство Кощи). Поэтому b ≥ 6 (d – целое, значит, d ≥ 1). Равенство достигается в случае, когда уравнение имеет четыре кратных корня, равных 1. В этом случае многочлен имеет вид
2 + 2 + 2 (неравенство Кощи). Поэтому b ≥ 6 (d – целое, значит, d ≥ 1). Равенство достигается в случае, когда уравнение имеет четыре кратных корня, равных 1. В этом случае многочлен имеет вид
(x – 1)4 = x4 – 4x3 + 6x² – 4x + 1.
Ответ
b = 6.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет