Задача
Дан фиксированный треугольник ABC. Пусть D – произвольная точка в плоскости треугольника, не совпадающая с его вершинами. Окружность с центром в D, проходящая через A, пересекает вторично прямые AB и AC в точках Ab и Ac соответственно. Аналогично определяются точки Ba, Bc, Ca и Cb. Точку D назовём хорошей, если точки Ab, Ac, Ba, Bc, Ca и Cb лежат на одной окружности.
Сколько может оказаться точек, хороших для данного треугольника ABC?
Решение
Очевидно, что центр O описанной окружности Ω треугольника ABC – хорошая точка, поскольку в этом случае Ba = Ca = A, Ab = Cb = B и
Ac = Bc = C.
Рассмотрим теперь любую хорошую точку D, отличную от O. Пусть A', B', C' – проекции D на BC, CA, AB соответственно. Точки A и Ab симметричны относительно C', так же как и точки B и Ba. Значит, середины отрезков AB и AbBa также симметричны относительно C'; следовательно, серединный перпендикуляр к AbBa проходит через точку O', симметричную O относительно D (рис. слева). Аналогично, серединные перпендикуляры к AcCa и BcCb также проходят через O', при этом они не параллельны; значит, O' и является центром окружности, проходящей через шесть точек. Заметим, что O' также не совпадает с D.
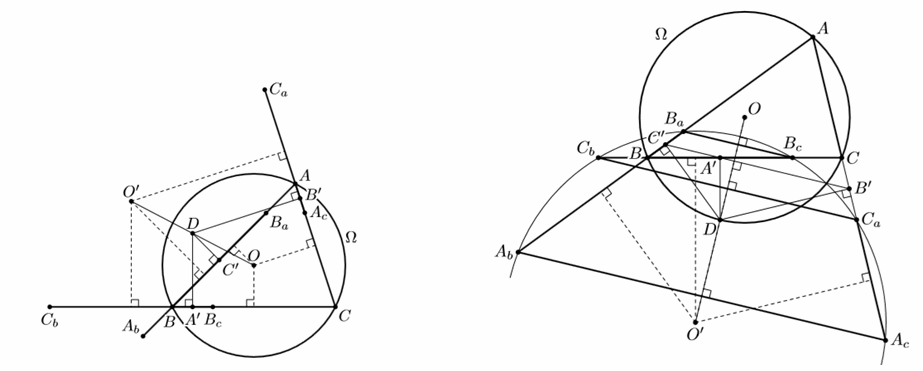
Ответ
2, 3 или 4.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь