Задача
Решите систему ![]()
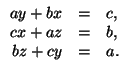 Какой геометрический смысл она имеет?
Какой геометрический смысл она имеет?
Решение
1) Пусть abc ≠ 0. Умножим первое уравнение на c, прибавим второе, умноженное на b, и вычтем третье, умноженное на a. Получим
2bcx = c² + b² – a². Аналогично находятся y и z.
2) Если a = b = 0, то и с = 0, а x, y, z – любые числа.
3) Если a = 0, b, с ≠ 0, то bx = c, (b² – c²)x = 0, следовательно, при b = ± c x = ±1, а в остальных случаях решений нет. Из последнего уравнения
y ± z = 0.
Ответ
При abc ≠ 0 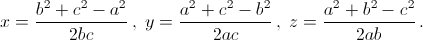 При a = 0, если b = с ≠ 0, то (x, y, z) = (1, t, – t); если b = – с ≠ 0, то (x, y, z) = (1, t, t).
При a = 0, если b = с ≠ 0, то (x, y, z) = (1, t, – t); если b = – с ≠ 0, то (x, y, z) = (1, t, t).
При b = 0, если a = с ≠ 0, то (x, y, z) = (t, 1, – t), если a = – с ≠ 0, то (x, y, z) = (t, 1, t).
При c = 0, если a = b ≠ 0, то (x, y, z) = (t, – t, 1), если a = – b ≠ 0, то (x, y, z) = (t, t, 1).
При a = b = с = 0, x, y, z – любые числа.
В остальных случаях решений нет.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь