Задача
Найдите cos 36° и cos 72°.
Решение
Пусть cos 36° = x. Первый способ. Заметим, что cos 72° = 2x² – 1. Кроме того, cos 36° – cos 72° = 2sin 54° sin 18° = 2cos 36° cos 72°, то есть
x – (2x² – 1) = 2x(2x² – 1) ⇔ 4x³ + 2x² – 3x – 1 = 0 ⇔ (x + 1)(4x² – 2x – 1) = 0.
Это уравнение имеет три корня: 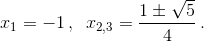 Поскольку cos 36° > 0, нас устраивает только один из них.
Поскольку cos 36° > 0, нас устраивает только один из них.
cos 72° находится из равенства cos 72° = 2x2 – 1. Второй способ. Рассмотрим равнобедренный треугольник ABC с основанием BC = 1 и углом при вершине A, равным cos 36°. Проведём биссектрису BK и заметим, что ∠ABK = ∠A = 36°, ∠BKC = ∠C = 72°. Значит, AK = BK = BC = 1, а AB = 2cos 36° = 2x. По свойству биссектрисы AB : BC = AK : KC, то есть 2x = 1/2x–1. Вновь получаем уравнение 4x² – 2x – 1 = 0.
Кроме того, BC = 2AB cos 72°, то есть 2cos 36° cos 72° = 1, откуда находится cos 72°. Третий способ. Рассмотрим правильный пятиугольник ABCDE со стороной 1. Его диагонали равны 2cos 36° = 2x. Пусть диагонали AC и BT пересекаются в точке K. Тогда CDEK – ромб, а AKB – равнобедренный треугольник с углом 36° при основании AB и боковой стороной, равной 2x – 1. В силу подобия треугольников AKB и ABC, вновь получаем уравнение 2x/1 = 1/2x–1.
Ответ
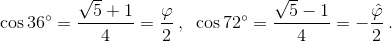
Чтобы оставлять комментарии, войдите или зарегистрируйтесь