Задача
Пусть a, b, c – стороны треугольника, p – его полупериметр, а r и R – радиусы вписанной и описанной окружностей соответственно. Составьте уравнение с коэффициентами, зависящими от p, r, R, корнями которого являются числа a, b, c. Докажите равенство
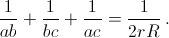
Решение
a + b + c = 2p, abc = 4RS = 4Rrp (см. задачу 208568). Отсюда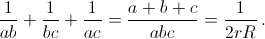 
. По формуле Герона
r2p2 = p(p – a)(p – b)(p – c), то есть r2p = p3 – (a + b + c)p2 + (ab + bc + ac)p – abc = p3 – 2p3 + (ab + bc + ac)p – 4Rrp. Значит,
ab + bc + ac = r2 + p2 + 4Rr. Теперь уравнение записывается по обратной теореме Виета.
Ответ
x3 – 2px2 + (r2 + p2 + 4Rr)x – 4Rrp = 0.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет