Задача
Решите системы: а) 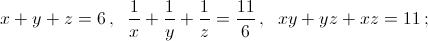 б) x(y + z) = 2, y(z + x) = 2, z(x + y) = 3; в) x2 + y2 + x + y = 32, 12(x + y) = 7xy;
г)
б) x(y + z) = 2, y(z + x) = 2, z(x + y) = 3; в) x2 + y2 + x + y = 32, 12(x + y) = 7xy;
г) 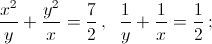 д) x + y + z = 1, xy + xz + yz = –4, x3 + y3 + z3 = 1; е) x2 + y2 = 12, x + y + xy = 9.
д) x + y + z = 1, xy + xz + yz = –4, x3 + y3 + z3 = 1; е) x2 + y2 = 12, x + y + xy = 9.
Решение
а) Из последних двух уравнений следует, что xyz = 6. Таким образом, x, y, z определены однозначно с точностью до перестановки. Но одно решение – (1, 2, 3) – очевидно. б) Вычитая первые два уравнения, получаем xz = yz. Поскольку z ≠ 0 (это видно из последнего уравнения), то x = y. Тогда из последнего уравнения xz = 3/2. Подставляя в первое уравнение, получаем x2 = 1/2. в) Положим u = x + y, v = xy. Тогда уравнения запишутся в виде u2 + u – 2v = 32, 12u = 7v. Подставляя v из второго уравнения в первое, получим 7u2 – 17u – 224 = 0, откуда u1 = 7, u2 = – 32/7. Соответственно, v1 = 12, v2 = – 384/49. В первом случае x, y – корни квадратного уравнения t2 – 7t + 12 = 0, то есть {x, y} = {3, 4}; во втором получаем квадратное уравнение 49t2 + 224t – 384 = 0. Его корни равны 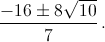 г) Уравнения можно записать в виде 2(x3 + y3) = 7xy, 2(x + y) = xy. Поделив первое уравнение на второе, получим x2 – xy + y2 = 7. Положим u = x + y, v = xy. Тогда
u2 – 3v = 7, 2u = v. Подставляя, получим u2 – 6u – 7 = 0, откуда u1 = 7, u2 = – 1. Соответственно,
г) Уравнения можно записать в виде 2(x3 + y3) = 7xy, 2(x + y) = xy. Поделив первое уравнение на второе, получим x2 – xy + y2 = 7. Положим u = x + y, v = xy. Тогда
u2 – 3v = 7, 2u = v. Подставляя, получим u2 – 6u – 7 = 0, откуда u1 = 7, u2 = – 1. Соответственно,
v1 = 14, v2 = – 2. Уравнение t2 – 7t + 14 = 0, соответствующее первому случаю корней не имеет; во втором получаем квадратное уравнение t2 + t – 2 = 0. Его корни равны 1 и –2. д) Одно решение – {1, 2, –2} – очевидно. Других решений нет – см. решение задачи 161039. е) Положим u = x + y, v = xy. Тогда уравнения запишутся в виде u2 – 2v = 12, u + v = 9. Подставляя, получим u2 + 2u – 30 = 0, откуда
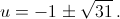 x, y – корни квадратного уравнения вида t2 – ut + (9 – u) = 0, то есть равны
x, y – корни квадратного уравнения вида t2 – ut + (9 – u) = 0, то есть равны 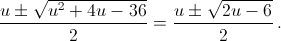 Подкоренное выражение положительно только при первом значении
Подкоренное выражение положительно только при первом значении 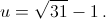
Ответ
а) {1, 2, 3}; б) 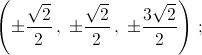 в)
в) 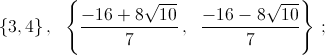 г) {1, –2}; д) {1, 2, –2}; е)
г) {1, –2}; д) {1, 2, –2}; е) 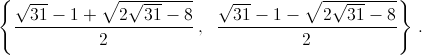
Чтобы оставлять комментарии, войдите или зарегистрируйтесь