Задача
Постройте многочлен, корни которого равны квадратам корней многочлена x3 + x2 – 2x – 1.
Решение
Пусть f(x) = x3 + x2 – 2x – 1. Поскольку f(–1) = 1, а f(0) = –1, то f(x) имеет три действительных корня u, v, w. Первый способ. По теореме Виета σ1 = u + v + w = – 1, σ2 = uv + uw + vw = – 2, σ3 = uvw = 1. Согласно решению задачи 161030
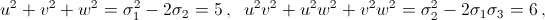
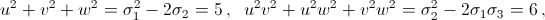
g(t2) = (t2 – u2)(t2 – v2)(t2 – w2) = (t + u)(t + v)(t + w)(t – u)(t – v)(t – w) = – f(– t)f(t) =
= (t3 – t2 – 2t + 1)(t3 + t2 – 2t – 1) = (t3 – 2t)2 – (t2 – 1)2 = t2(t2 – 2)2 – (t2 – 1)2.
Значит, g(x) = x(x – 2)2 – (x – 1)2 = x3 – 4x2 + 4x – (x2 – 2x + 1) = x3 – 5x2 + 6x – 1.
Ответ
x3 – 5x2 + 6x – 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет