Задача
Найдите все значения параметра a, при которых корни x1, x2, x3 многочлена x3 – 6x2 + ax + a удовлетворяют равенству
(x1 – 3)3 + (x2 – 3)3 + (x3 – 3)3 = 0.
Решение
Согласно задаче 161030 б)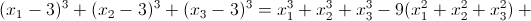 
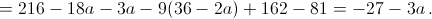Это выражение равно нулю при a = – 9.
Однако многочлен x3 – 6x2 – 9x – 9 имеет только один действительный корень. Действительно, его производная 3x2 – 12x – 9 имеет корни разного знака, то есть функция достигает локального максимума в некоторой точке x0 < 0. Но трёхчлен 6x2 + 9x + 9 корней не имеет, поэтому x3 – 6x2 – 9x – 9 < 0 при x < 0.
Ответ
Таких a не существует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет