Задача
Найдите все значения параметра r, при которых уравнение (r – 4)x² – 2(r – 3)x + r = 0 имеет два корня, причём каждый из них больше –1.
Решение
Заметим, что r ≤ 4.
Проверим условие положительности дискриминанта: (r – 3)² – r(r – 4) > 0 ⇔ 9 – 2r < 0 ⇔ r > 4,5.
При этих значениях r ветви параболы направлены вверх и абсцисса вершины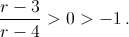 
Кроме того, значение трёхчлена в точке –1 положительно: (r – 4) + 2(r – 3) + r = 4r – 10 > 0.
Следовательно, при всех r > 4,5 оба корня больше –1.
Ответ
r > 4,5.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет