Заметим, что  a ≠ – 1.

  Дискриминант  9a² – 16a(1 + a) > 0,  поэтому  7a² + 16a < 0.  Тем самым область значений a сужается до интервалов  (– ¹⁶/₇, –1)  и  (– 1, 0).

  Далее, абсцисса вершины параболы должна быть больше 1: 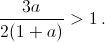    Решение этого неравенства сужает область значений a до  (– ¹⁶/₇, –1).   При таких значениях a ветви параболы направлены вниз. Поэтому значение трёхчлена в точке 1 должно быть отрицательно:  (1 + a) – 3a + 4a = 2a + 1 < 0.  Это условие выполнено на всем указанном интервале.

При  – ¹⁶/₇ < a < – 1.