Задача
Пусть x1, x2 – корни уравнения x² + px + q = 0. Выразите через p и q следующие выражения:
а) 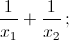 б)
б) 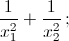 в)
в) 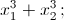 г)
г) 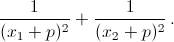
Решение
Решение 1:а) 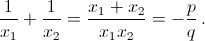 б)
б) 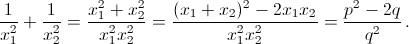 в)
в) 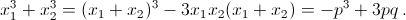 г)
г) 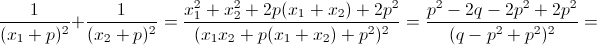
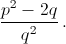
Решение 2:а) Запишем уравнение в виде 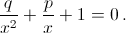 Отсюда видно, что 1/x1 и 1/x2 – корни уравнения qt² + pt + 1 = 0. По формуле Виета их сумма равна – p/q. б) Из исходного уравнения следует другое: (x² + q)² = (px)². Отсюда видно, что
Отсюда видно, что 1/x1 и 1/x2 – корни уравнения qt² + pt + 1 = 0. По формуле Виета их сумма равна – p/q. б) Из исходного уравнения следует другое: (x² + q)² = (px)². Отсюда видно, что 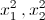 – корни уравнения t² + (2q – p²)t + q² = 0.
– корни уравнения t² + (2q – p²)t + q² = 0.
Согласно а) 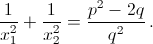 г) x1 + p и x² + p – корни уравнения (x – p)² + p(x – p) + q = 0, то есть уравнения x² – px + q = 0. Согласно б)
г) x1 + p и x² + p – корни уравнения (x – p)² + p(x – p) + q = 0, то есть уравнения x² – px + q = 0. Согласно б) 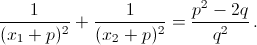
Ответ
а) – p/q; в) 3pq – p3; б), г) 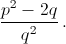
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет