Задача
Докажите, что если Pn/Qn (n ≥ 1) – подходящая дробь к числу α, то имеет место по крайней мере одно из неравенств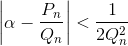 
или 
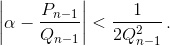Получите отсюда теорему Валена: для любого α найдётся бесконечно много таких дробей p/q, что |α – p/q| < 1/2q2.
Решение
Разберём случай чётного n (тогда Pn/Qn ≤ α < Pn–1/Qn–1). Пусть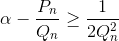 
и 
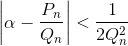Тогда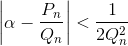 
(неравенство Коши строгое, поскольку Qn ≠ Qn–1). Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет