Задача
Пусть a, b и c – длины сторон треугольника площади S; α1, β1 и γ1 – углы некоторого другого треугольника. Докажите, что
a² ctg α1 + b² ctg β1 + c² ctg γ1 ≥ 4S, причём равенство достигается, только когда рассматриваемые треугольники подобны.
Решение
Пусть x = ctg α1 и y = ctg β1. Тогда x + y > 0 (так как α1 + β1 < π и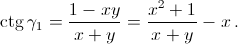 
Поэтому 
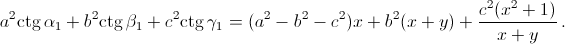При фиксированном x это выражение минимально при таком y, что 
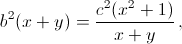то есть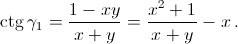 
Аналогичные рассуждения показывают, что если a : b : c = sin α1 : sin β1 : sin γ1, то рассматриваемое выражение минимально. В этом случае треугольники подобны и a² ctg α + b² ctg β + c² ctg γ = 4S (см. задачу 157627, б)).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет