Задача
В параллелограмм P1 вписан параллелограмм P2, а в параллелограмм P2 вписан параллелограмм P3, стороны которого параллельны сторонам P1. Докажите, что длина хотя бы одной из сторон P1 не превосходит удвоенной длины параллельной ей стороны P3.
Решение
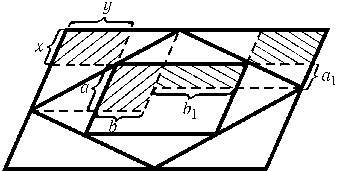
Введем такие обозначения, как на рисунке. Все рассматриваемые параллелограммы имеют общий центр (задача 156462). Длины сторон параллелограмма P3 равны a + a1 и b + b1, а длины сторон параллелограмма P1 равны a + a1 + 2x и b + b1 + 2y, поэтому нужно проверить, что
a + a1 + 2x ≤ 2(a + a1) или b + b1 + 2y ≤ 2(b + b1), то есть 2x ≤ a + a1 или 2y ≤ b + b1. Предположим, что a + a1 < 2x и b + b1 < 2y. Тогда
≤ ½ (a + a1) < x и 
< y. С другой стороны, равенство площадей заштрихованных параллелограммов (см. задачу 156769) показывает, что
ab = xy = a1b1, а
значит, · = xy. Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь