Обозначим центр многоугольника через O, вершины – через   A₁, ..., A_n.  Предположим, что среди одноцветных многоугольников нет равных, то есть они имеют  m = m₁ < m₂ < ... < m_k  сторон соответственно. Рассмотрим преобразование, определенное на множестве вершин n-угольника и переводящее каждую вершину A_i в вершину  A_i' = A_mi  (считаем, что  A_p+n = A_p).  При этом преобразовании вершины правильного m-угольника переходят в одну точку B, поэтому сумма векторов 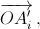   где A_i – вершины m-угольника, равна   m ≠ 0.

  Вершины правильного p-угольника переходят друг в друга при повороте на угол ^360°/_p вокруг точки O, поэтому их образы при нашем преобразовании переходят друг в друга при повороте на угол ^360°m/_p. Этот угол меньше 360° при  p > m.  Поэтому и суммы векторов 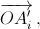   как по всем вершинам n-угольника, так и по вершинам m₂-, m₃-, ..., m_k-угольников равны нулю. Значит, и сумма таких векторов по вершинам m-угольника равна нулю. Противоречие.

Ответ задачи отсутствует