Задача
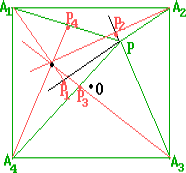
Внутри квадрата A1A2A3A4 взята точка P. Из вершины A1 опущен перпендикуляр на A2P, из A2 — перпендикуляр на A3P, из A3 — на A4P, из A4 — на A1P. Докажите, что все четыре перпендикуляра (или их продолжения) пересекается в одной точке.
Решение
При повороте вокруг центра квадрата на 90o, переводящем точку A1 в точку A2, перпендикуляры, опущенные из вершин A1, A2, A3, A4, переходят в прямые A2P, A3P, A4P и A1P соответственно. Поэтому точкой их пересечения является образ точки P при обратном повороте.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет