Олимпиадная задача по математике: решение алгебраического уравнения для 8-9 класса
Задача
Решите уравнение: 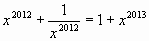 .
.
Решение
Воспользуемся тем, что a + a–1 ≥ 2 при а > 0 (см. эадачу 130861).
Заметим, что x = 1 является корнем данного уравнения и докажем, что других корней нет. Действительно, если x < 1, то x2012 + x–2012 ≥ 2 > 1 + x2013; а если x > 1,  то  x2012 < x2013,  а  x–2012 < 1. В обоих случаях равенство невозможно.
Ответ
x = 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет