Олимпиадная задача по планиметрии для 10–11 класса: отрезок KN на окружности
Задача
Точка Х расположена на диаметре АВ окружности радиуса R. Точки K и N лежат на окружности в одной полуплоскости относительно АВ,
а ∠KXA = ∠NXB = 60°. Найдите длину отрезка KN.
Решение
Рассмотрим точку K', симметричную точке K относительно диаметра АВ (см. рисунок). Она лежит на той же окружности и ∠KXA = 60°. Тогда сумма трёх углов с вершиной в точке Х (отмеченных на чертеже) равна 180°. Следовательно, точки K', X и N лежат на одной прямой.
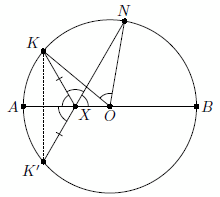
Ответ
KN = R.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет