Олимпиадная задача по планиметрии: угол в треугольнике AMC, 9–10 класс
Задача
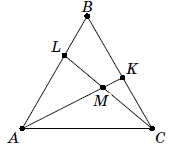
На сторонах AB и BC равностороннего треугольника ABC отмечены точки L и K соответственно, M – точка пересечения отрезков AK и CL. Известно, что площадь треугольника AMC равна площади четырёхугольника LBKM. Найдите угол AMC.
Решение
Из равенства площадей треугольника AMC и четырёхугольника LBKM следует равенство площадей треугольников ACK и CBL (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет