Олимпиадная задача: Размещение натуральных чисел по вершинам квадрата для классов 9–10
Задача
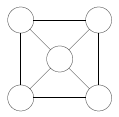
Расставьте в кружках, расположенных в вершинах квадрата и в его центре, пять натуральных чисел так, чтобы каждые два числа, соединенные отрезком, имели общий делитель, больший 1, а любые два числа, не соединенные отрезком, были бы взаимно просты.
Решение
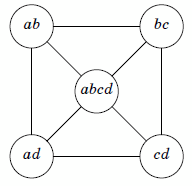
Возьмём четыре попарно взаимно простых числа a, b, c, d и запишем в двух противоположных вершинах квадрата числа ab и cd, в других вершинах – числа ad и bc, а в центре – abcd (см. рис.).
Ответ
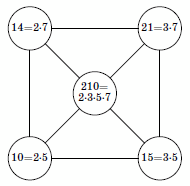
Например:
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет