Олимпиадная задача: разрезание сыра на равные части с использованием отношения a : (1 – a)
Задача
Продавец хочет разрезать кусок сыра на части, которые можно будет разложить на две кучки равного веса. Он умеет разрезать любой кусок сыра в одном и том же отношении a : (1 – a) по весу, где 0 < a < 1. Верно ли, что на любом промежутке длины 0,001 из интервала (0, 1) найдётся значение a, при котором он сможет добиться желаемого результата с помощью конечного числа разрезов?
Решение
Назовём число a подходящим, если 0 < a < 1 и для этого значения a продавец сможет добиться желаемого результата. Пусть число a подходящее, тогда число 1 – a также является подходящим. Докажем, что подходящим будет также 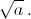 Для этого достаточно показать как разрезать кусок сыра веса 1 на части в отношении a : (1 – a), используя разрезы в отношении
Для этого достаточно показать как разрезать кусок сыра веса 1 на части в отношении a : (1 – a), используя разрезы в отношении 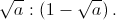
После первого разреза у нас появится кусок веса 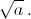 Разрезав его, мы получим два куска, вес одного из которых равен a. Значит, второй кусок в сумме с куском, оставшимся от первого разреза, весит 1 – a.
Разрезав его, мы получим два куска, вес одного из которых равен a. Значит, второй кусок в сумме с куском, оставшимся от первого разреза, весит 1 – a.
То, что часть весом 1 – a оказалась не целой, а составленной из двух, несущественно: при необходимости дальнейшего разрезания этой составной части мы сможем разрезать в нужном отношении каждую из составляющих её частей. Поэтому в дальнейшем мы такую кучку будем рассматривать как один кусок.
Число a0 = ½ является подходящим. Следовательно, подходящими являются и числа 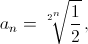 а также числа bn = 1 – an. Заметим, что
а также числа bn = 1 – an. Заметим, что
1,5 < bn–1/bn = 1 + an < 2.
Числа 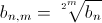 также подходящие. Поскольку (1 + 0,001)1024 > 1 + 1024·0,001 > 2, имеем
также подходящие. Поскольку (1 + 0,001)1024 > 1 + 1024·0,001 > 2, имеем
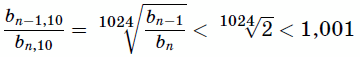 и
и 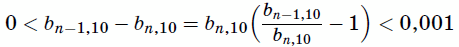 .
.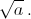 Так как bn–1/bn> 1,5, найдётся такое натуральноеN, что bN< 0,0011024 и, следовательно, bN,10< 0,001.
В наборе подходящих чисел bN,10<bN–1,10< ... <b0,10 первое число меньше 0,001, последнее больше 0,999 и разности между соседними числами меньше 0,001. Поэтому этот набор имеет непустое пересечение с каждым из промежутков длины 0,001 из интервала (0, 1).
Так как bn–1/bn> 1,5, найдётся такое натуральноеN, что bN< 0,0011024 и, следовательно, bN,10< 0,001.
В наборе подходящих чисел bN,10<bN–1,10< ... <b0,10 первое число меньше 0,001, последнее больше 0,999 и разности между соседними числами меньше 0,001. Поэтому этот набор имеет непустое пересечение с каждым из промежутков длины 0,001 из интервала (0, 1).
Ответ
Верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь