Олимпиадная задача по планиметрии: Биссектриса в трапеции, классы 8–10
Задача
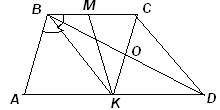
В трапеции ABCD биссектриса тупого угла B пересекает основание AD в точке K – его середине, M – середина BC, AB = BC.
Найдите отношение KM : BD.
Решение
Так как ∠ABK = ∠CBK = ∠BKA, то треугольник ABK – равнобедренный: AK = AB = BC. Тогда ABCK – ромб. Так как KD = AK = BC, то BCDK – также параллелограмм.
Ответ
1 : 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет