Олимпиадная задача по планиметрии: параллелограмм ONHM в остроугольном треугольнике
Задача
В остроугольном треугольнике АВС угол В равен 45°, АМ и CN – высоты, О – центр описанной окружности, Н – ортоцентр.
Докажите, что ОNHМ – параллелограмм.
Решение
Решение 1: Проведём серединные перпендикуляры к сторонам АВ и ВС данного треугольника. Они пересекаются в точке О (рис. слева). Так как в прямоугольном треугольнике BNC ∠NBC = 45°, то BN = NC. Следовательно, NO || HM. Аналогично MO || HN. Таким образом, ONHM – параллелограмм.
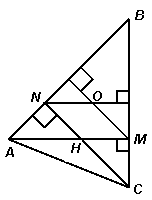
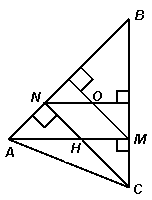
Решение 2: Рассмотрим окружность, описанную около треугольника АВС (рис. справа). Так как этот треугольник – остроугольный, то её центр O лежит внутри треугольника, причём треугольник АОС – равнобедренный и ∠AOC = 2∠ABC = 90°. Следовательно, точки N, O и M лежат на окружности с диаметром AC.
Тогда ∠ONC = ∠OAC = 45°, ∠ONВ = ∠ВNC – ∠ONC = 45° и ∠МАВ = 90° – ∠АВМ = 45°. Из равенства углов ONВ и МАВ следует параллельность прямых NO и AM. Аналогично доказывается, что MO || CN.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь