Докажите неравенство с суммой квадратов: олимпиадная задача по алгебраическим неравенствам
Задача
Докажите, что если x > 0, y > 0, z > 0 и x² + y² + z² = 1, то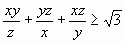 
, и укажите, в каком случае достигается равенство.
Решение
Пусть S = xy/z + yz/x + xz/y, тогда S² = (xy/z)² + (yz/x)² + (xz/y)² + 2x² + 2y² + 2z² ≥ 3x² + 3y² + 3z² = 3 (мы воспользовались неравенством
a² + b² + c² ≥ ab + bc + ac, равенство в котором достигается, когда а = b = c, см. задачу 130865).
Следовательно,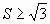 
. Равенство достигается, когда 
.
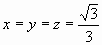Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет