Олимпиадная задача по планиметрии с правильным треугольником, окружностями и углом BOC
Задача
Две окружности с радиусами 1 и 2 имеют общий центр в точке O. Вершина A правильного треугольника ABC лежит на большей окружности, а середина стороны BC – на меньшей. Чему может быть равен угол BOC?
Решение
Решение 1:
Рассмотрим случай, когда точки O и A лежат в одной полуплоскости относительно прямой BC (рис. слева).Пусть K – середина BC, G – точка пересечения медиан треугольника ABC. Продолжим отрезок OK до пересечения с большей окружностью в точке O1. Тогда K – середина также отрезка OO1, поэтому BOCO1 – параллелограмм. G – точка пересечения медиан также треугольника AOO1, поскольку AK – медиана этого треугольника, и AG : GK = 2 : 1. А так как этот треугольник равнобедренный, то медиана OG является также биссектрисой, откуда следует равенство треугольников AGO и O1GO. Следовательно, GO1 = GA = GB = GC, то есть точки A, B, C, O1 лежат на окружности с центром G. Поэтому ∠BO1C = 180° – ∠A = 60°.
Аналогично рассматривая второй случай, получим ∠BO1C = 120°.
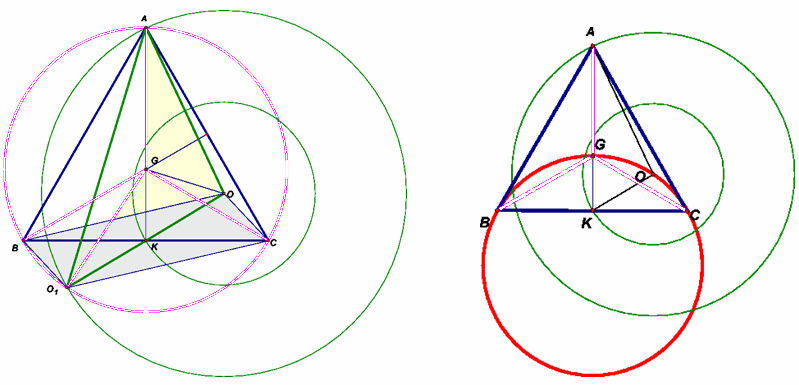
Решение 2:
используем те же обозначения.Из условия следует, что AG : KG = AB : KB = AC : KC = AO : KO = 2 : 1. Значит, точки B, G, O, C лежат на окружности Аполлония для отрезка АК (рис. справа). Понятно также, что ∠BGC = ∠BOC или 180° – ∠BOC.
Ответ
60° или 120°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь