Олимпиадная задача по планиметрии: восстановление треугольника ABC по точкам W и O
Задача
Вокруг треугольника ABC описали окружность Ω. Пусть L и W – точки пересечения биссектрисы угла A со стороной BC и окружностью Ω соответственно. Точка O – центр описанной окружности треугольника ACL. Восстановите треугольник ABC, если даны окружность Ω и точки W и O.
Решение
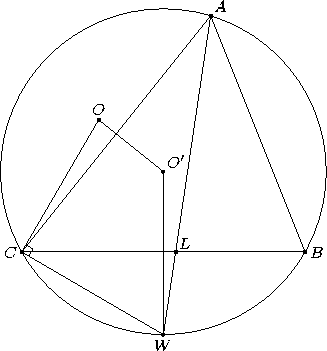
Пусть O' – центр Ω. Тогда прямые O'O и O'W перпендикулярны сторонам AC и BC, то есть направления этих сторон известны. Кроме того,
∠COL = 2∠CAL = 2∠LCW и, значит, ∠OCW = 90° (см. рис.). Следовательно, C – точка пересечения окружности Ω и окружности с диаметром OW.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет