Олимпиадная задача по планиметрии: равенство углов в треугольниках с вписанной окружностью
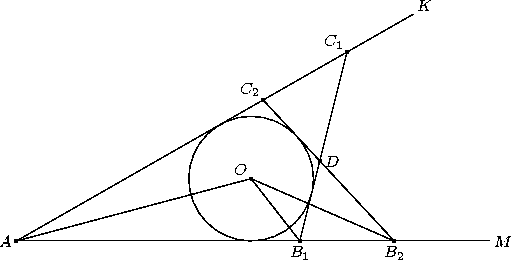
Задача
Точки B1 и B2 лежат на луче AM, а точки C1 и C2 на луче AK. Окружность с центром O вписана в треугольники AB1C1 и AB2C2.
Докажите, что углы B1OB2 и C1OC2 равны.
Решение
Пусть отрезки B1C1 и B2C2 пересекаются в точке D (см. рис.). Тогда по теореме о внешнем угле треугольника
∠B1OB2 = ∠AB1O – AB2O = ½ (∠AB1C1 – ∠AB2C2) = ½ ∠B1DB2. Аналогично ∠C1OC2 = ½ ∠C1DC2 = ½ ∠B1DB2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет