Олимпиадная задача по планиметрии и комбинаторной геометрии для 8-11 классов от Глазырина
Задача
Дано множество точек O, A1, A2, ..., An на плоскости. Расстояние между любыми двумя из этих точек является квадратным корнем из натурального числа. Докажите, что существуют
такие векторы x и y, что для любой точки Ai выполняется равенство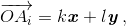 
где k и l – некоторые целые числа.
Решение
Из условия следует, что для любых i, j скалярное произведение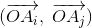 
является
половиной целого числа. Значит, для любых целых чисел m1, ..., mn длина вектора 
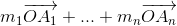– корень из натурального числа. Отметим на плоскости точки, являющиеся концами всех таких векторов. Пусть X – ближайшая к O из отмеченных точек, Y – ближайшая к O из отмеченных точек, не лежащих на прямой OX. Разобьём плоскость на параллелограммы, образованные векторам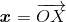и 
и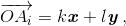 
В силу выбора точек X, Y все отмеченные точки будут вершинами параллелограммов разбиения, следовательно, векторы x, y – искомые.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь