Олимпиадная задача по планиметрии и неравенствам для 8–11 классов от Швецова Д. В.
Задача
Пусть a, b, c – длины сторон произвольного треугольника; p – полупериметр; r – радиус вписанной окружности. Докажите неравенство
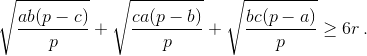
Решение
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет
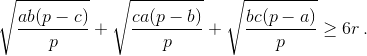 (R – радиус описанной окружности, S – площадь, см. задачи
(R – радиус описанной окружности, S – площадь, см. задачи