Олимпиадная задача по планиметрии и алгебраическим неравенствам Френкина и Кайранбай, 8-11 класс

Пусть A₁A₂... A_n – данный многоугольник, B₁, B₂, ..., B_n – точки касания вписанной окружности со сторонами A₁A₂, A₂A₃, ..., A_nA₁. Обозначим значения углов первого многоугольника через a₁, ..., a_n, а второго – через b₁, ..., b_n. Тогда  b_i = ½ (a_i + a_i+1).  Перемножая n таких равенств, получаем

2ⁿa₁a₂... a_n = (a₁ + a₂)...(a_n–1 + a_n)(a_n + a₁).  Но по неравенству Коши 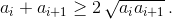    Поэтому из полученного равенства следует, что все углы многоугольников равны, а так как многоугольник B₁...B_n – вписанный, то многоугольники правильные.

Верно.