Олимпиадная задача по планиметрии: доказательство средней точки отрезка в треугольнике

  Как известно, если G – точка пересечения медиан некоторого треугольника XYZ, то для произвольной точки Р выполняется равенство: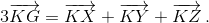  

  Рассмотрим векторы a, b и c, начало каждого из которых расположено в точке Р, а конец – на основании перпендикуляра, опущенного из точки Р на соответствующую сторону треугольника ABC. Нам нужно доказать, что 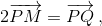    то есть, что  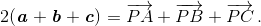   Для доказательства рассмотрим еще шесть векторов, каждый из которых лежит на прямой, параллельной стороне треугольника и проходящей через точку Р.

  Начало каждого такого вектора расположено в точкеР, а конец – на одной из сторон треугольника. (На рисунке изображен случай, когда точкаРлежит внутри треугольника.) Через эти векторы легко выразить как векторы, соединяющиеРс вершинами, так и векторы с концами в основаниях перпендикуляров – поскольку параллельные линии разбивают треугольник на правильные треугольники и параллелограммы. Из рисунка видно, что указанное равенство выполняется.   Легко убедиться в и том, что эти рассуждения проходят и в случае, когда точкаРрасположена вне треугольникаАВС.

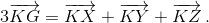
Ответ задачи отсутствует