Олимпиадная задача по планиметрии: квадраты и прямоугольники вокруг четырёхугольника

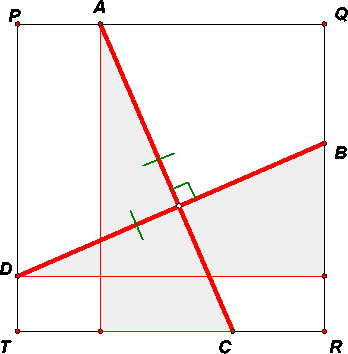
  Лемма. Пусть точки A и C лежат на одной паре противоположных сторон квадрата, а B и D - на другой. Тогда условия  AC ⊥ BD  и  AC = BD  являются равносильными (рис. слева).

 Доказательствосразу следует из равенства прямоугольных треугольников, показанных на рисунке.   Проведём в нашем четырёхугольнике, вписанном в два квадрата, из точки A прямую, перпендикулярную BD и отметим её точки пересечения с соответствующими сторонами квадрата: C₁ и C₂ (рис. справа).

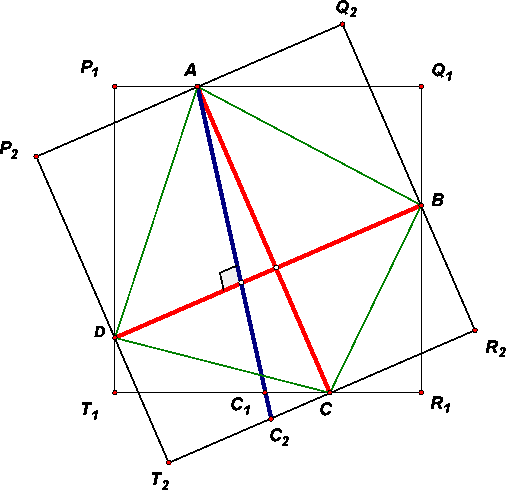
  Из леммы вытекает, что  AC₁ = BD  и  AC₂ = BD,  то есть точки C₁, C₂ совпадают. Но у двух сторон квадратов, содержащих эти точки, имеется только одна общая точка – C. Значит, построенный нами перпендикуляр совпадает с AC, и, следовательно, диагонали четырёхугольника ABCD равны и перпендикулярны. Очевидно, что если четырёхугольник с таким свойством вписан в прямоугольник, то прямоугольник является квадратом.

Верно.