Назад

Олимпиадная задача по планиметрии: закрашенные треугольники в треугольнике ABC для 8-9 класса

Задача 215735 • Сложность: 3 • 8-9 класс
Задача

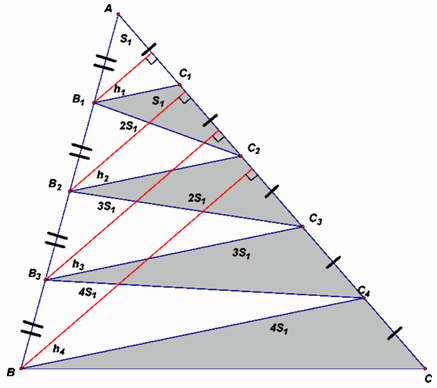
Сторону AB треугольника ABC разделили на n равных частей (точки деления  B0 = A,  B1, B2,  Bn = B),  а сторону AC этого треугольника разделили на

n + 1  равных частей (точки деления  C0 = A,  C1, C2, ..., Cn+1 = C).  Закрасили треугольники CiBiCi+1. Какая часть площади треугольника закрашена?

Авторы:
Хачатурян А. В.
Разделы:
Планиметрия
Источники:
I Олимпиада по геометрии имени И.Ф. Шарыгина (2005 г.) Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина Заочный тур
Количество версий:
5
Решение

  Покажем, что закрашенная часть составляет ровно половину площади всего треугольника. Для этого из точек B1, ..., Bn опустим перпендикуляры на сторону AC. Эти перпендикуляры являются высотами треугольников CiBiCi+1 с одинаковыми основаниями, причём, как следует из соображений подобия,  hi = ih1.  Отсюда вытекает, что таким же соотношением будут связаны площади окрашенных треугольников:  Si = iS1. (На рисунке изображен случай  n = 4.)

  Опустив затем перпендикуляры из точекC1, ...,Cnна сторонуAC, и рассуждая аналогично, получим такое же соотношение для площадей незакрашенных треугольников. Осталось заметить, что площадь первого закрашенного треугольника равна площади первого незакрашенного (их основания равны, а высотаh1общая).
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет