Олимпиадная задача по планиметрии для 9–10 класса: выпуклый n-угольник с равными синусами углов и разными сторонами

  Очевидно, треугольников с таким свойством не существует. Покажем, что не существует и четырёхугольников. Сделать это можно по-разному.   Первый способ. Так как синусы углов равны, то сами углы четырёхугольника равны либо φ, либо  180° – φ.  Перебором легко убедиться в том, что в этом случае мы имеем дело либо с прямоугольником, либо с параллелограммом, либо с равнобокой трапецией.   Второй способ. Рассмотрим выпуклый четырёхугольник, синусы всех углов которого равны, со сторонами длины a, b, c, d. Вычислив его площадь двумя способами, как сумму площадей двух треугольников, придём к соотношению  ab + cd = ad + bc  или  (a – c)(b – d) = 0.  Отсюда вытекает равенство, по крайней мере, одной пары сторон.   Чтобы построить пятиугольник, обладающий искомыми свойствами, достаточно отрезать у равнобокой трапеции с углом 60° при большем основании "уголок" (рис. слева).

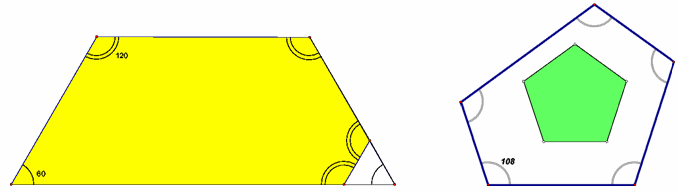
  Также можно взять правильный пятиугольник с углами 108° и с его помощью построить пятиугольник, все стороны которого соответственно параллельны сторонам правильного пятиугольника, но не равны между собой (рис. справа).

При   n = 5.