Олимпиадная задача Шарича В.: квадраты в сумме простых чисел, многочлены, 8–10 класс
Задача
Для каждого натурального n обозначим через Sn сумму первых n простых чисел: S1 = 2, S2 = 2 + 3 = 5, S3 = 2 + 3 + 5 = 10, ... .
Могут ли два подряд идущих члена последовательности (Sn) оказаться квадратами натуральных чисел?
Решение
Обозначим n-е простое число через pn. Предположим, что нашлось m > 1, для которого Sm–1 = k², Sm = n², где k и n – натуральные числа. Числа
S2 = 5, S3 = 10 квадратами не являются, так что m > 4. Заметим, что pm = Sm – Sm–1 = (n – k)(n + k); ввиду простоты pm получаем 1 = n – k,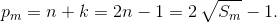 
Таким образом,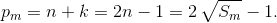 
Заметим, что pm нечётно (так как m > 2), и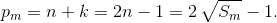 
С другой стороны, в сумму Sm = 2 + p² + ... + pm, кроме двойки, входят лишь нечётные числа, и при m > 4 не входят нечётное составное число 9 и число 1, поэтому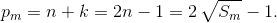 
Противоречие.
Ответ
Не могут.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь