Олимпиадная задача на многочлены и неравенства для 8-9 класса, автор Агаханов Н. Х.
Задача
Даны квадратные трёхчлены x² + 2a1x + b1, x² + 2a2x + b2, x² + 2a3x + b3. Известно, что a1a2a3 = b1b2b3 > 1.
Докажите, что хотя бы один из этих трёхчленов имеет два корня.
Решение
Предположим противное; тогда дискриминанты всех трёхчленов неположительны, то есть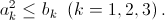 
Левые (а значит, и правые) части этих неравенств неотрицательны, поэтому их можно перемножить: (a1a2a3)² ≤ b1b2b3 = a1a2a3. Но это противоречит неравенству a1a2a3 > 1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет