Олимпиадная задача Богданова И. И. — дистанция между числами в квадрате 100×100

  Пронумеруем в квадрате строки (снизу вверх) и столбцы (слева направо) числами от 1 до 100; будем обозначать клетку парой номеров её строки и столбца. Назовём расстоянием между клетками расстояние между их центрами. Клетки назовём парными, если числа в них различаются на 5000. Заметим, что расстояние от клетки  (50, 50)  до любой другой (в частности, до парной ей) не превосходит 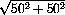  = 50 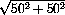.  Значит, и минимальное расстояние между парными клетками также не превосходит  50 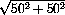.  Осталось привести пример, когда этот минимум достигается.

  Разобьём наш квадрат на четыре квадрата 50×50. Расставим числа от 1 до 2500 согласно правилам в левом нижнем квадрате так, чтобы число 1 стояло в клетке  (1, 1),  а число 2500 – в клетке  (50, 1)  (это возможно; например, первые 50 чисел в первом столбце, вторые – во втором и т. д.). Далее, если число  a ∈ [1, 2500]  стоит в клетке  (i, k),  то поставим числа  a + 2500,  a + 5000  и  a + 7500  соответственно в клетки  (k + 50, i),

(k + 50, i + 50)  и  (51 – i, 101 – k).  Нетрудно видеть, что при этом числа по-прежнему расставлены согласно правилам (для соседних чисел в одном квадрате это очевидно; для чисел 2500-2501, 5000-5001 и 7500-7501 проверяется непосредственно).

  Осталось проверить, что расстояния между парными клетками не меньше  50 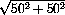.  Рассмотрим отрезок между любыми парными клетками. Сумма его горизонтальной и вертикальной проекций равна либо  (50 + k – i) + (50 + i – k) = 100,  либо  (k + 50 – 51 + i) + (101 – k – i) = 100,  то есть она всегда равна 100. Значит, квадрат длины этого отрезка равен  x² + (100 – x)² = 2(x – 50)² + 5000 > 5000 = (50 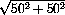)²,  что и требовалось.

  Ниже приведён пример аналогичной расстановки в квадрате 8×8.

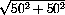
Ответ задачи отсутствует